2차 방정식 근을 구하는 함수 코딩해보기

#수학 #코딩 #함수계산기 #계산기 #SimpleMath #2차방정식문제

함수계산기는 자바스크립트와 비슷한 코딩문법을 가진 SimpleMath라 불리는 스크립트를 이용하여 자기만의 수학함수를 만들 수 있습니다.

이번에는 2차 방정식 ax^2+bx+c=0 의 해를 구하는 함수를 만들어 봅시다.
이번에도 chatgpt에게 함수계산기 코딩스크립트인 SimpleMath를 써서 ax^2+bx+c=0 의 해를 구하는 함수를 만들어 달라고 요청했습니다. 만약 해가 없으면 -515151.515151을 반환하라고 지시했습니다.
이래는 chatgpt가 짜 준 함수 코드입니다.

def solveQuadratic(a,b,c,xy){
  var D=b*b−4*a*c;
  if(D<0){
    return -515151.515151;
  }
  var sqrtD=sqrt(D);
  if(xy==1){
    return (-b+sqrtD)/(2*a);
  }
  return (-b−sqrtD)/(2*a);
}

함수이름이 영어라서 친숙하지 않을 땐 기존 영어이름 함수를 아래 코딩과 같이 한글이름 함수로 바꿔 줄 수 있습니다.

def 이차방정식(a,b,c,선택)=solveQuadratic(a,b,c,선택);

위 함수는 앞서 만들었던 영어이름의 함수를 사용하여 한글이름이 이차방정식인 새 함수를 만든 것입니다.
파라미터 a와 b와 c는 각각 2차 방정식의 계수들이고 파라미터 '선택'은 신호를 주는 값으로 두 근 중 첫째를 구하려면 1을 두번째 근을 구하려면 2를 주도록 설정하는 파라미터입니다.

위 함수 2개를 복사한 후 함수계산기의 공장페이지로 가서 페이지  오른쪽 상단에  점점점 메뉴버튼을 눌러 붙여넣기를 클릭해서 코드창에 코드를 붙여놓은 후 run버튼을 눌러 코드를 실행을 하고 save버튼을 눌러 실행된 함수를 DB에 저장하세요.
그 다음에 계산기 페이지로 와서 F2버튼을 누르면 방금 만든 함수를 선택해서 계산에 이용할 수 있습니다.
-2x^2+3x+1=0의 해를 아래  그림2개와 같이 구할 수 있습니다.

여러가지 2차 함수 해를 방금 만든 함수를 사용해서 위 예시처럼  구할 수 있습니다.

만약 파라미터가 너무 많아서 헷갈리는 경우엔 공장페이지에서 계산할 수 있습니다.
공장페이지에서 F2버튼을 길게 누르면 F2버튼이 FN2버튼으로 바뀝니다. 그리고 함수를 선택하면 파라미터  이름이 모두 표기된 함수가 코드창에 뜨게됩니다. 각 파라미터  오른쪽 = 기호 다음에 적당한 값을 입력한 다음 닫기괄호를 입력하고 run버튼을 누르면 공장페이지에서 함수를 아래 그림과 같이 실행할 수 있습니다.

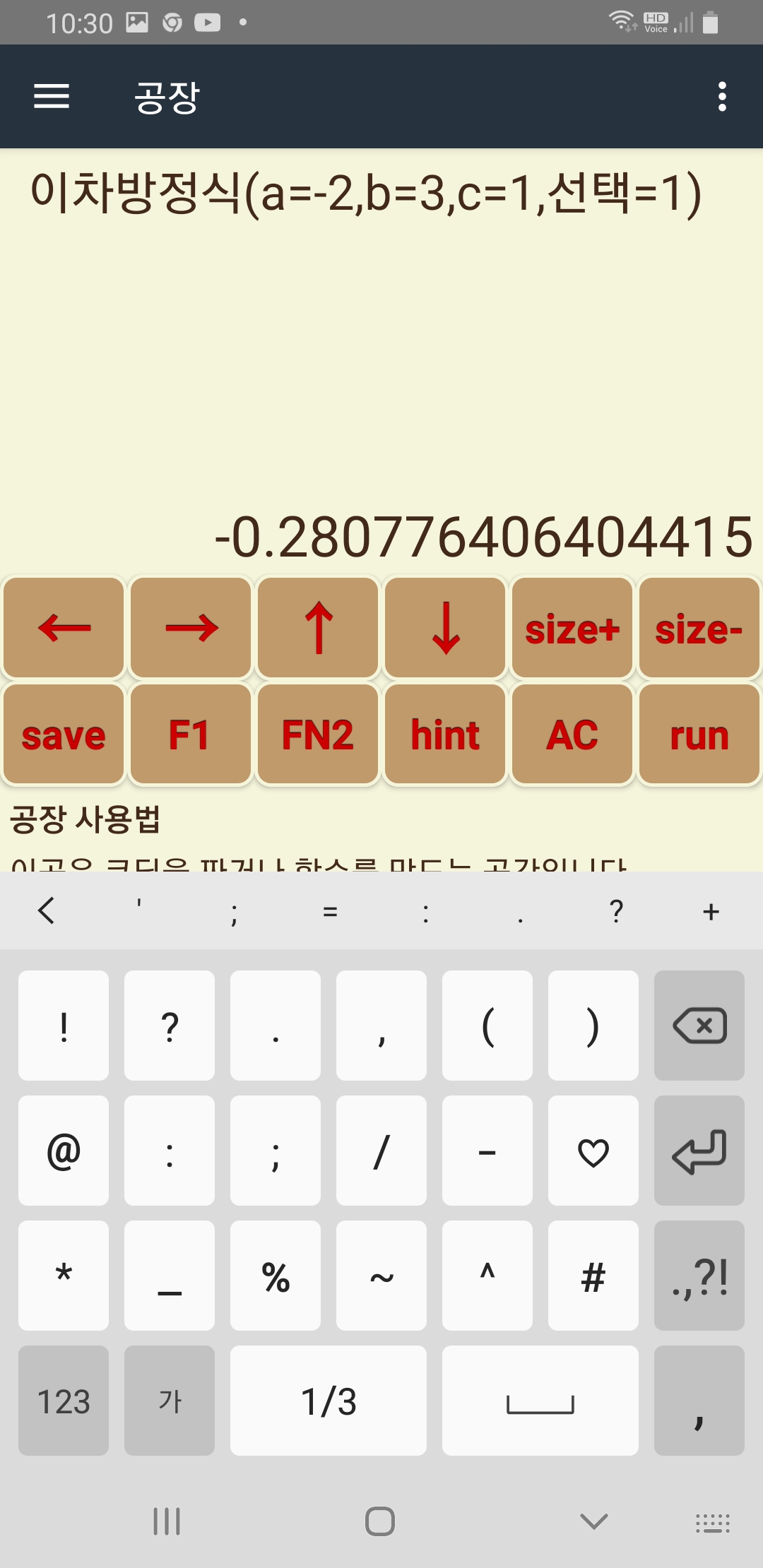
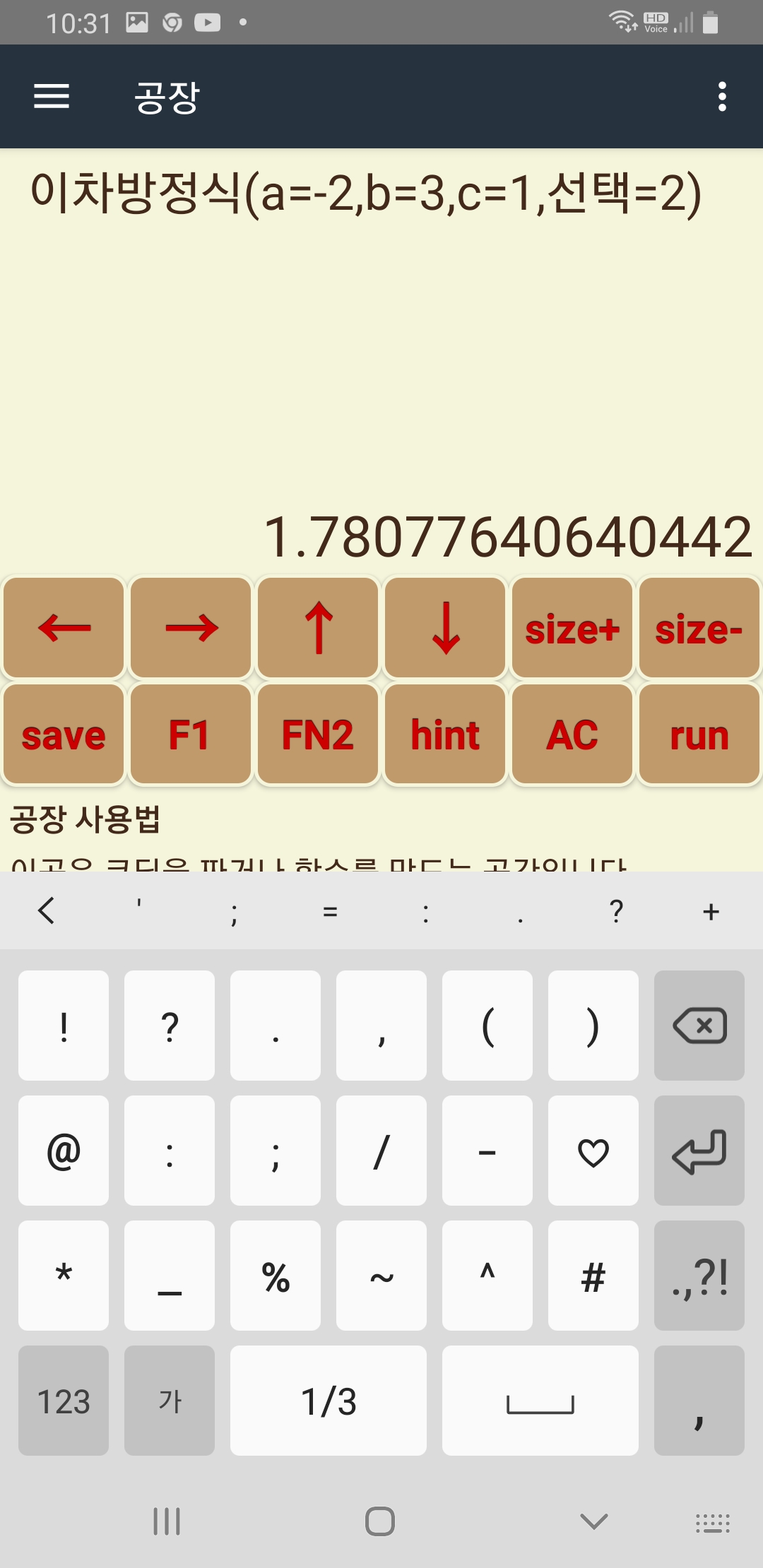
문제) x^2+2x+1=0 의 두 해를 위에서 만든 함수를 사용해 구하시오.

허근을 포함하는 2차 방정식을 푸는 함수 만들어 보기

위에서는 실수 해만을 구하는 함수 코딩이었고
이번에는 허근의 경우까지 포함하는 함수를 아래와 같이 코딩할 수 있습니다.
아래는 AI에게 요청해서 얻은 코딩입니다.

def iSolveQuadraticAI(a,b,c,x12,real){
  if(a==0){
    return -515151;
  }
  var D=b*b−4*a*c;
  var sqrtD=sqrt(abs(D));
  var realPart=-b/(2*a);
  var imaginaryPart=sqrtD/(2*a);
  if(D<0){
    if(real==1){
      return realPart;
    }
    if(x12==1){
      return imaginaryPart;
    }
    return -imaginaryPart;
  }
  if(real!=1){
    return 0;
  }
  if(x12==1){
    return realPart+sqrtD/(2*a);
  }
  return realPart−sqrtD/(2*a);
}

앞서의 경우와 마찬가지로 한글이름 함수도 위 함수를 이용해 만들겠습니다.

def 이차방정식복소해(a,b,c,선택,실허)=iSolveQuadraticAI(a,b,c,선택,실허);

이번에도 역시 앞서 설명한 방법대로 위 코드  2개를 공장페이지 코드창에 복사해서 붙여넣은 다음 run버튼을 눌러 실행하고 save 버튼을 눌러 저장합니다.  
그런 후 계산기로 돌아와 F2버튼을 눌러 계산에 이용합니다.

x^2+2x+8의 해를 아래 그림과 같이 구할 수 있습니다.

위 그림으로 부터 x^2+2x+8의 두 해는 하나는 -1+2.645751 i 이고 다른 하나는 그것의 켤레복소수인 것을 알 수 있습니다.

위 함수는 만약 구하는 해가 실근이면 허수부분 값을 0으로 반환하기때문에 모든 2차방정식 풀이에 사용될 수 있습니다.

함수계산기를 다운받아 여러가지 수학문제를 코딩으로 해결해보세요.