2025. 3. 27. 15:25ㆍ함수계산기
이번에는 정적분의 근사값을 자동계산하는 함수를 함수계산기의 공장페이지에서 코딩해 보도록 하겠습니다.
리만합에 대한 쉽고 자세한 나용은 여기를 참조하시기 바랍니다.
이런 함수는 한 번 만들어 두면 수학공부할 때 정적분의 답을 계산하거나 아님 여러가지 적분 계산에 쉽게 이용할 수 있습니다.
먼저 리만합을 구할 대상이 되는 함수를 f(x)라 하면
아래와 같이 코딩을 할 수 있을 것입니다.
아래는 코사인 함수의 정적분의 근사치를 구하는 코딩입니다.
def f(x) = cos(x);
def RiemannSum(start,end){
var Sn=0;
var n=2000;
var delta=(end−start)/n;
var k=1;
while(k<=n){
var x=start+delta*(k−0.5);
var h=f(x);
var s=delta*h;
Sn=Sn+s;
k=k+1;
}
var round6=round(Sn*10^6)/10^6;
return round6;
}
간단히 코딩을 설명하면
먼저 대상이 되는 함수 f(x)를 코사인 함수로 지정을 했습니다.
다른 함수의 정적분값을 구하는 함수를
만드려면 f(x) 에 해당하는 함수를 = 을 써서 지정해 주면 됩니다.
그 다음에는 구분구적을 구하는 함수를 본격적으로 만듭니다.
변수 Sn은 구분구적 사각형들의 넓이의 합을 나타내고
delta 는 등분된 작은 사각형의 가로길이
start 는 정적분 시작점
end 는 정적분 마지막 점
n 은 2000 등분으로 설정했고
k 는 n등분된 구간 중 k번째
s는 k번째 작은 사각형의 넓이를 나타냅니다.
마지막에 round 함수를 사용해 답이 보기 좋게 나오도록 정리해서 계산된 값을 산출하도록 세팅합니다.
함수계산기의 공장페이지에다 위 코딩을 복사해 붙여넣고 run버튼을 눌러 코드를 실행하세요.
나중에도 계속 만든 함수를 사용하려면 save 버튼을 눌러 저장하세요.
아래 그림과 같이 cos(x)의 정적분의 근사치를 구할 수 있습니다.

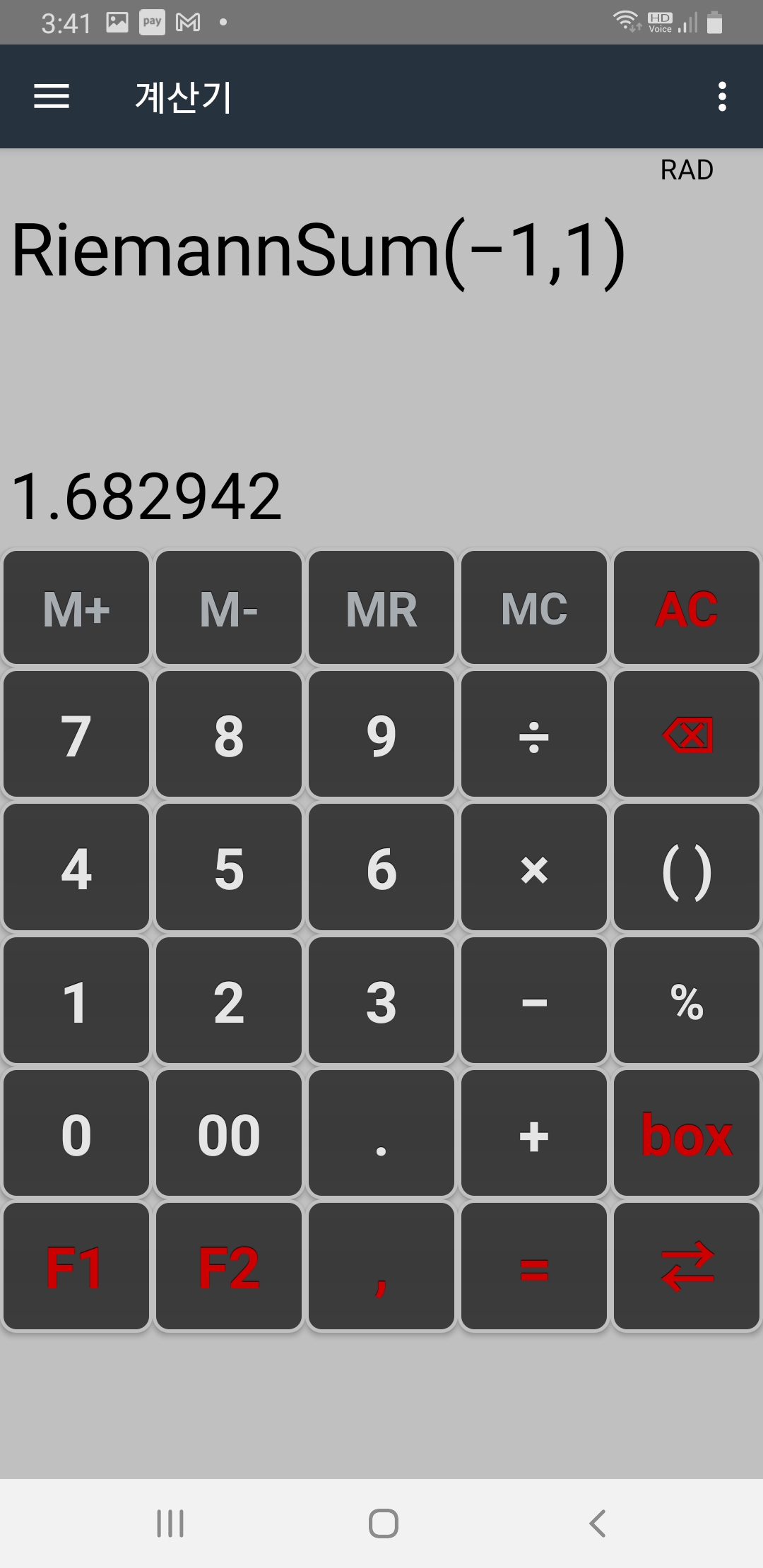
만약 cos(x) 대신 가령 3*x^2−5*x+7에 대한 정적분 값을 구하려면 기존 f(x) 함수를 내함수 목록에서 지운후 새로 def f(x)=3*x^2−5*x+7; 를 코딩해서 실행한 후 아래와 같이 f(x)의 정적분 값을 구할 수 있습니다.
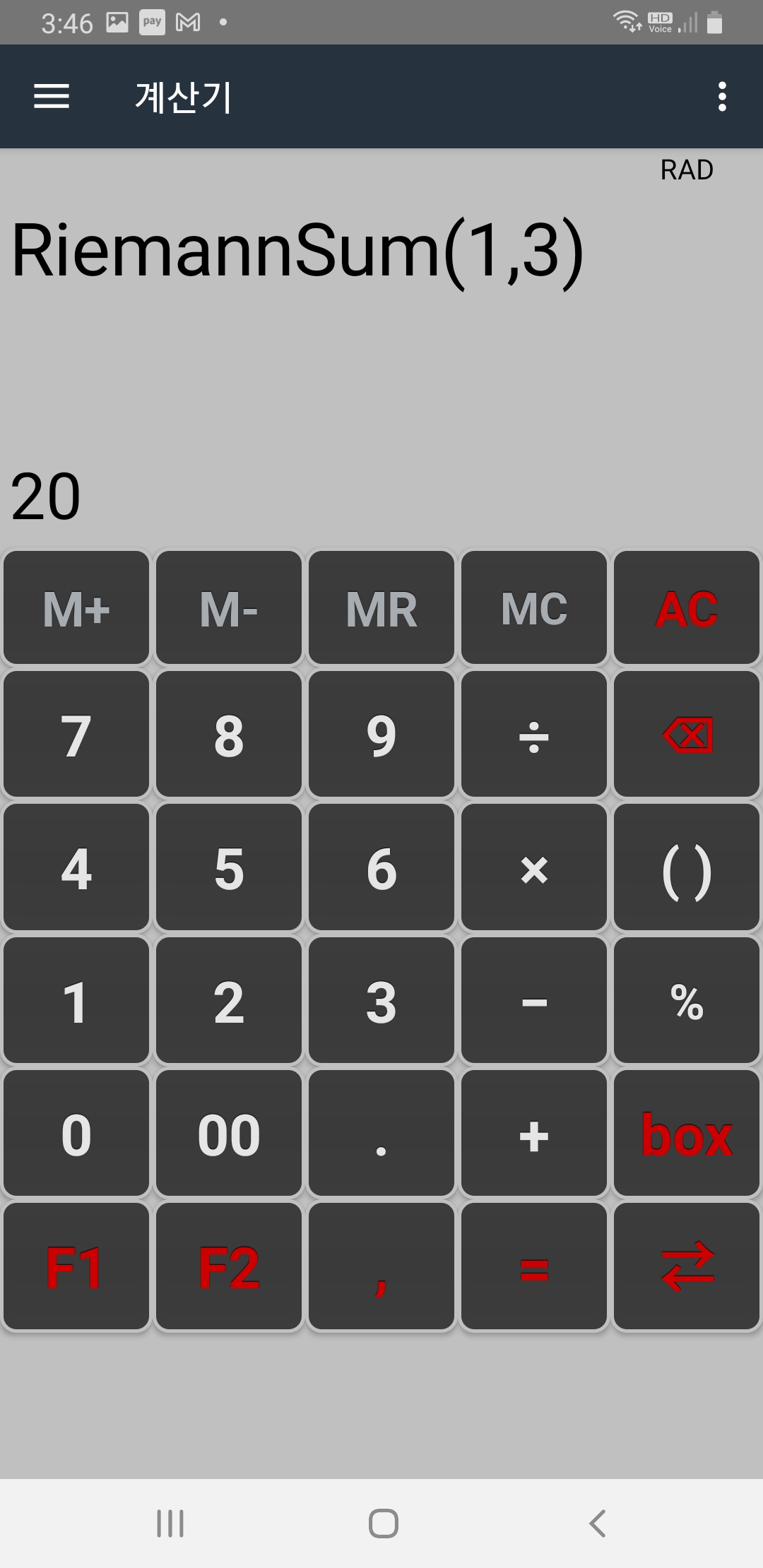
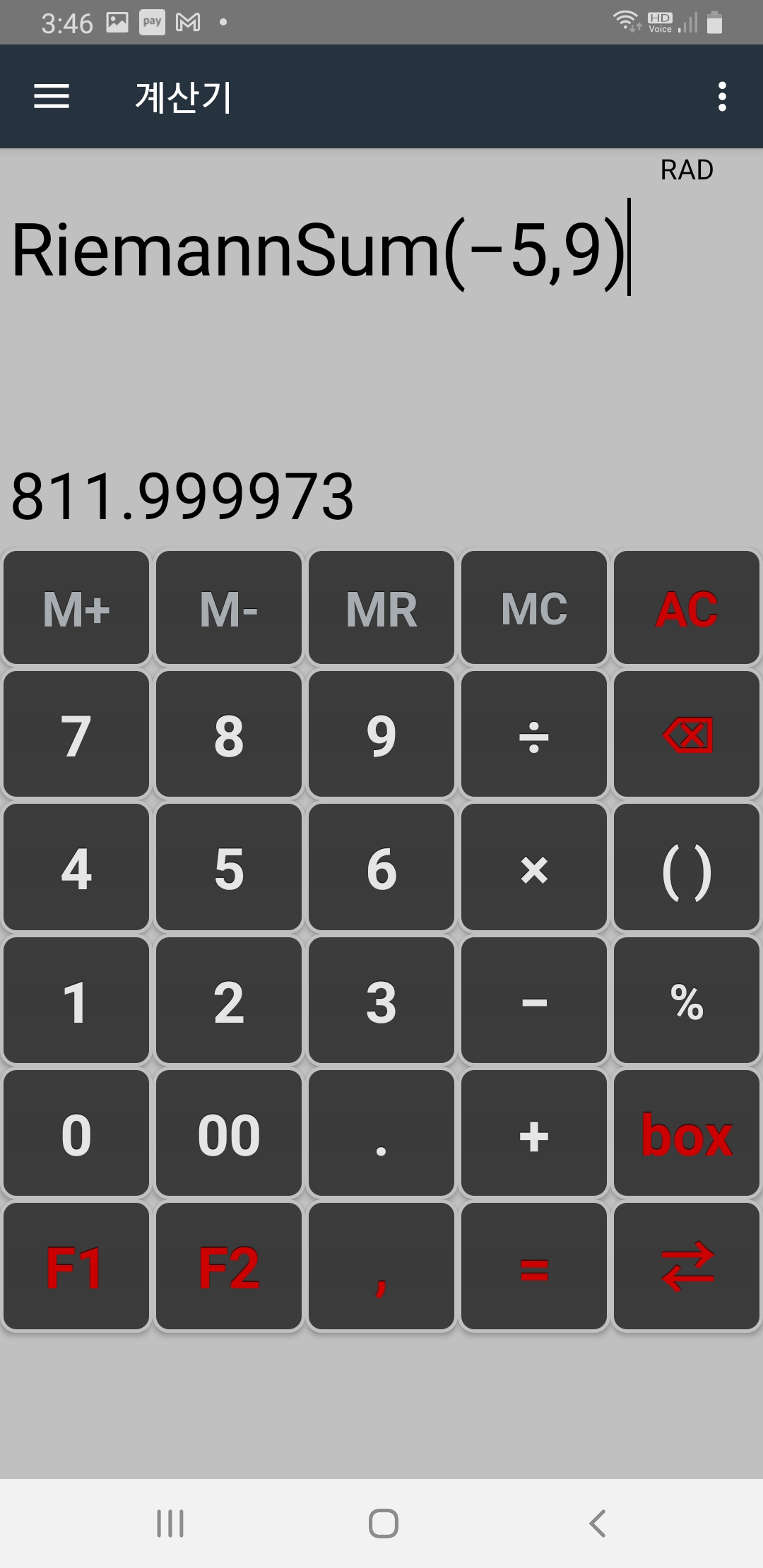
칸아카데미 사이트에서 예시로 든 f(x)=(1/5)*x^2 의 2에서 6까지 리만합을 구해보면 아래 그림과 같습니다.
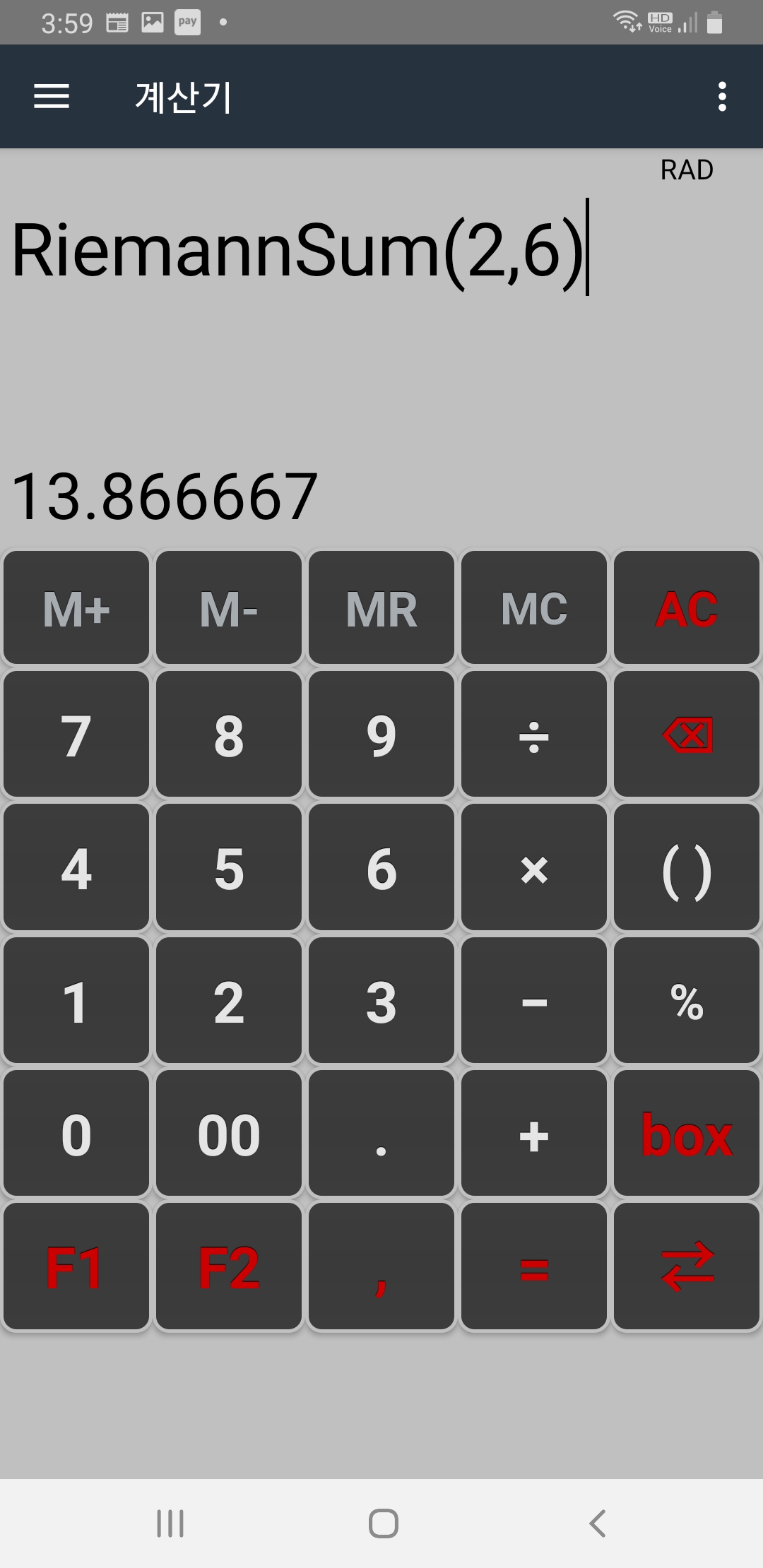
함수계산기를 활용하여 다른 많은 수학함수도 코딩해 보시기 바랍니다.
'함수계산기' 카테고리의 다른 글
| 할부금 계산하는 함수 만들어 보기 (0) | 2025.03.28 |
|---|---|
| 생활 속의 연립방정식 (0) | 2025.03.28 |
| 최대공약수 와 최소공배수 계산 함수 (0) | 2025.03.24 |
| 한 근은 몇 그램? (0) | 2025.03.23 |
| 물체의 자유낙하 거리 계산 (2) | 2025.03.20 |