2025. 3. 31. 11:44ㆍ함수계산기
하노이 탑 퍼즐은 수학과 컴퓨터 과학에서 재귀 알고리즘을 학습하는 재료로 많이 사용되고 또 실제 하노이탑 퍼즐 푸는 게임도 있습니다.
하노이탑에 대한 자세한 설명은 위키백과에 잘 나와 있습니다.
여기서는 함수계산기의 코딩방식을 써서 하노이탑에 원반을 모두 옮기려면 몇 번을 옮겨야 하는가와 원반이 어떤 막대에서 어떤 막대로 옮겨가는지를 추적하는 함수를 만드는데 집중하도록 하겠습니다.
먼저 n개의 원반을 모두 옮기려면 몇 번을 옮겨야 하는지를 탐구해 봅시다.
하노이 탑 퍼즐은 3 개의 원반을 꽂을 수 있는 막대가 있는데 현재 모든 원반이 꽂혀있는 원반을 출발막대라 부르고 최종적으로 원반들이 옮겨 갈 막대를 도착막대 라 부르고 중간에 임시로 원반들을 옮겨 놓을 막대를 보조막대라 부릅시다.
여기서는 n개의 원반이 주어졌을 때 출발막대에서 도착막대로 모든 원반을 하노이탑의 규칙에 따라 옮길 때 최소 옮기는 횟수를 계산하는 함수를 재귀적으로 만들어 보는데 초점을 맞추겠습니다.
하노이탑 규칙은 아래와 같습니다.
오직 한 번에 원반 하나씩만 옮길 수 있다.
큰 원반은 작은 원반 위에 놓이면 안된다.
모든원반들은 보조막대를 사용하여 출발 막대로 부터 도착 막대로 옮겨야 한다.(땅에 놓으면 안된다는 뜻)
자 이 규칙에 따라 원반을 옮기는 로직을 만들어 보면 아래와 같습니다.
- 출발막대의 맨 밑 원반만 빼고 나머지 (n-1) 개의 원반을 보조막대로 옮긴다.
- 출발막대의 맨 밑 원반을 도착막대로 옮긴다.
- 보조막대에 꽂혀있는 (n-1) 개의 원반을 도착막대로 옮긴다.
끝
진짜로?
이렇게 간단하다고?
녜 이렇게 간단합니다.
위와 같은 로직을 재귀로직이라 부릅니다.
재귀로직에서는 가령 위의 예에서처럼 출발막대에서 보조막대로 (n-1)개의 원반을 옮길 때 몇 번 옮겨야하는지도 보조막대에서 도착막대로 (n-1) 개의 원반을 옮길 때 몇번 옮겨야 하는지에 대한 어떤 구체적 정보도 없습니다.
유일하게 구체적인 정보는 출발막대의 맨 밑의 원반을 도착막대로 옮길 때 1회 옮긴다는 정보가 전부입니다.
하지만 신기하게도 재귀는 이 유일한 하나의 정보만 가지고 모든 원반의 옮기는 횟수를 계산할 수 있습니다.
그 비밀은 재귀 즉 자기자신의 로직을 다시 사용하는데 있습니다.
가령 앞 서 얘기한 출발막대에서 보조막대로 (n-1) 개의 원반을 옮긴다는 로직은 자체적으로 출발막대를 출발막대로 놓고 보조막대를 도착막대로 놓고 도착막대를 보조막대로 놓고 (n-1) 개를 n으로 놓은 다음 부모 로직을 다시 사용하게 됩니다. 이 때도 반드시 구체적인 정보가 하나 얻어집니다. 즉 모든 실행마다 그 실행의 (n-1) 개를 옮기는 자식 로직이 있고 언제나 맨 밑 원반을 하나 최종적으로 옮기는 구체적인 정보가 반드시 있습니다. 이 매 하위로직마다 있는 최종원반 하나 옮기는 정보가 존재하고 이게 합산되기때문에 결국 총 몇 회 옮겨야하는 지가 계산되는 것입니다.
잘 생각해보세요.
알쏭달쏭하지만 잘 생각해보면 아하 하는 감이 올 것입니다.
자 위의 로직을 함수계산기의 코딩방식으로 코딩하면 아래와 같은 함수를 만들 수 있습니다.
def 하노이(n, 출발, 도착, 보조)
=하노이(n−1, 출발, 보조, 도착)
+ 1
+하노이(n−1, 보조, 도착, 출발);
하노이(1,출발,도착,보조)=1;
위 코드는 2개입니다.
첫째 코드 def 에서 시작해서 ; 으로 끝나는 부분은 함수의 정의 부분입니다.
앞서 로직을 함수 만드는 코딩으로 전환한 것입니다.
두번째 코드는 재귀함수의 베이스 조건에 해당합니다.
위의 함수로직이 무한 실행되는 것을 차단하는 초기조건을 규정한 코드입니다.
위 코드를 복사해서 함수계산기의 공장페이지에 붙여넣고 run 버튼을 눌러서 코딩을 실행하고 save 버튼을 눌러서 함수를 저장하세요.
그런 후 계산기 페이지로 넘어 와 F2버튼을 눌러 방금 만든 함수를 계산에 사용할 수 있습니다.
전설에 따르면 64개의 원반을 다 옮기면 세상에 종말이 온다고 하는데 아래 그림은 64개의 원반을 옮길 때 몇 번 옮겨야 하는지를 계산한 모습입니다.

이만큼 옮기려면 1초당 1개씩 쉬지 않고 옮긴다해도 우주나이인 138억년의 42배나 긴 시간이 지나야 세상의 종말이 온다는 게 되니 너무 걱정하지 않아도 될 듯 합니다. ^^
원반 추적하기
위에서는 몇 번 옮겨야 하는가에 초점을 맞췄다면 여기서는 원반이 어떤 막대에서 어떤 막대로 옮겨지는가를 추적하는 함수를 만들어 보도록 하겠습니다.
여기서도 위와 같이 재귀로직을 써서 함수를 만들 수 있습니다.
여기서는 출발막대를 1이라 놓고 도착막대를 2라 놓고 보조막대를 3이라 놓읍시다.
그리고 만약 출발막대에서 도착막대로 원반이 옮겨질 때는 12로 표기하고 출발막대에서 보조막대로 옮겨지면 13으로 도착막대에서 보조막대로는 23, 도착막대에서 출발막대로는 21, 보조막대에서 출발막대로는 31, 보조막대에서 도착막대로는 32와 같이 표기된다고 놓읍시다.
그렇게 되면 가령 1223은 원반이 출발막대에서 도착막대로 옮겨간 경우와 원반이 도착막대에서 보조막대로 옮겨간 두 가지 사건을 표기하는 셈입니다.
이렇게 추적하는 함수는 아래와 같이 코딩할 수 있습니다.
def 하노이추적(n,출발,도착,보조){
if(n==1){
return 출발*10+도착;
}
var 보도=하노이추적(n−1,보조,도착,출발);
var k=floor(log10(보도));
var 출도=출발*10^(k+2)+도착*10^(k+1);
var 출보=하노이추적(n−1,출발,보조,도착)*10^(k+3);
return 출보+출도+보도;
}
이해의 편의를 위해 파라미터 출발은 1이고 파라미터 도착은 2 파라미터 보조는 3이라 가정합시다.
이 때 위 코드의 의미는
원반이 하나이면 12를 산출하고
그 이상일 때는 출발막대에서 보조막대로 옮기는 추적치에다 맨 밑 원반의 출발막대에서 도착막대로 옮기는 추적치 12를 갖다 붙이고 그 다음 보조막대에서 도착막대로 옮기는 추적치를 뒤에 갖다 붙인다는 코딩이 되겠습니다.
위 코드를 복사해서 함수계산기의 공장페이지에 붙여넣은 후 run버튼을 눌러 실행하고 save 버튼을 눌러 저장하세요.
그 후 계산기 페이지에서 F2버튼을 눌러 아래 그림처럼 방금 만든 함수를 계산에 사용할 수 있습니다.
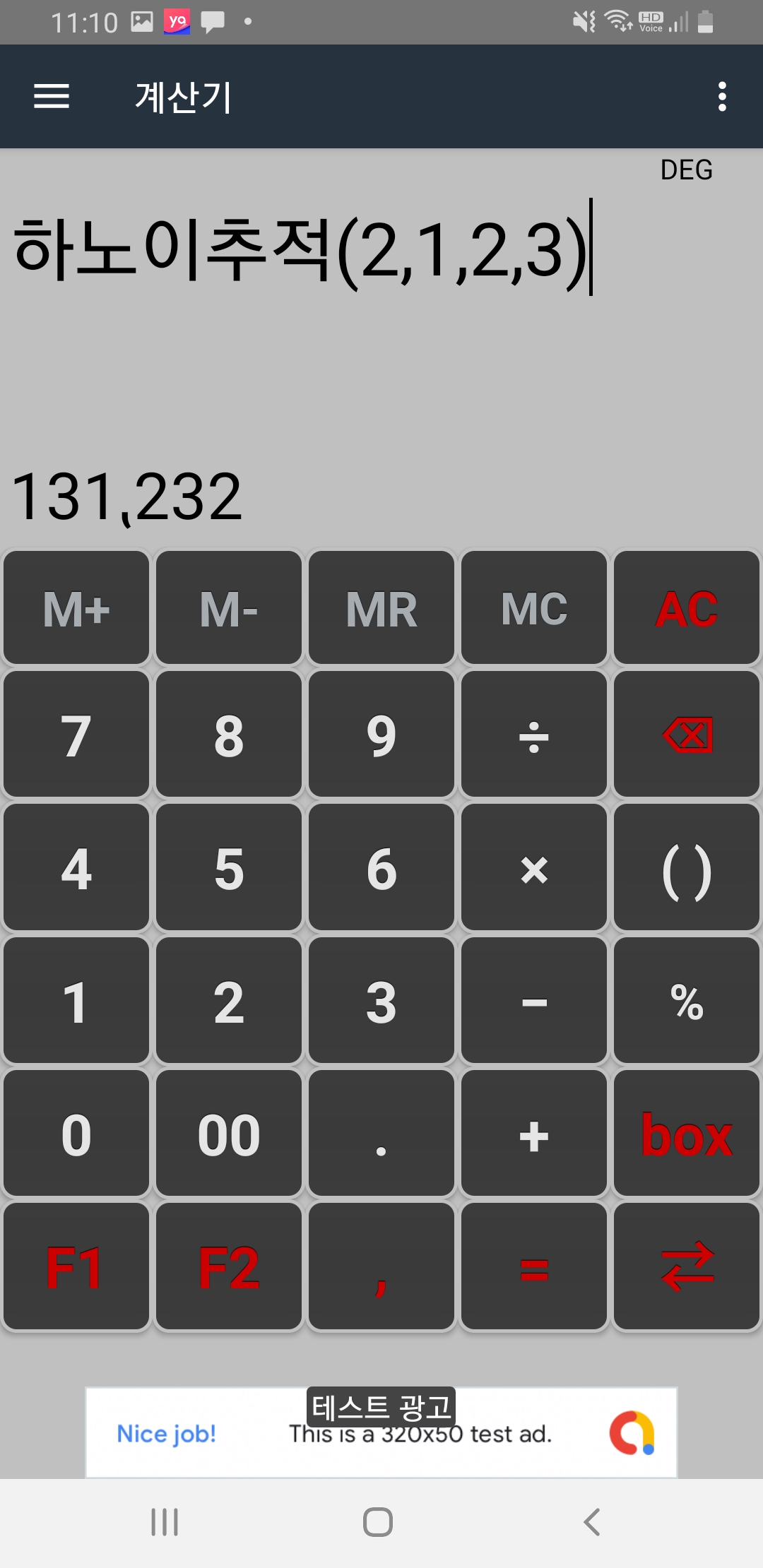
위 그림의 131232 는 13 12 32 로 띄어 읽을 수 있습니다. 즉 원반이 2개일 때 막대 1의 꼭대기 원반을 막대 3으로 옮기고 그 다음 막대 1의 꼭대기 원반을 막대 2로 옮기고 그 다음 막대 3의 원반을 막대 2로 옮겨야 된다는 의미입니다.
만약 원반이 3 개이면 아래와 같은 결과가 나옵니다.
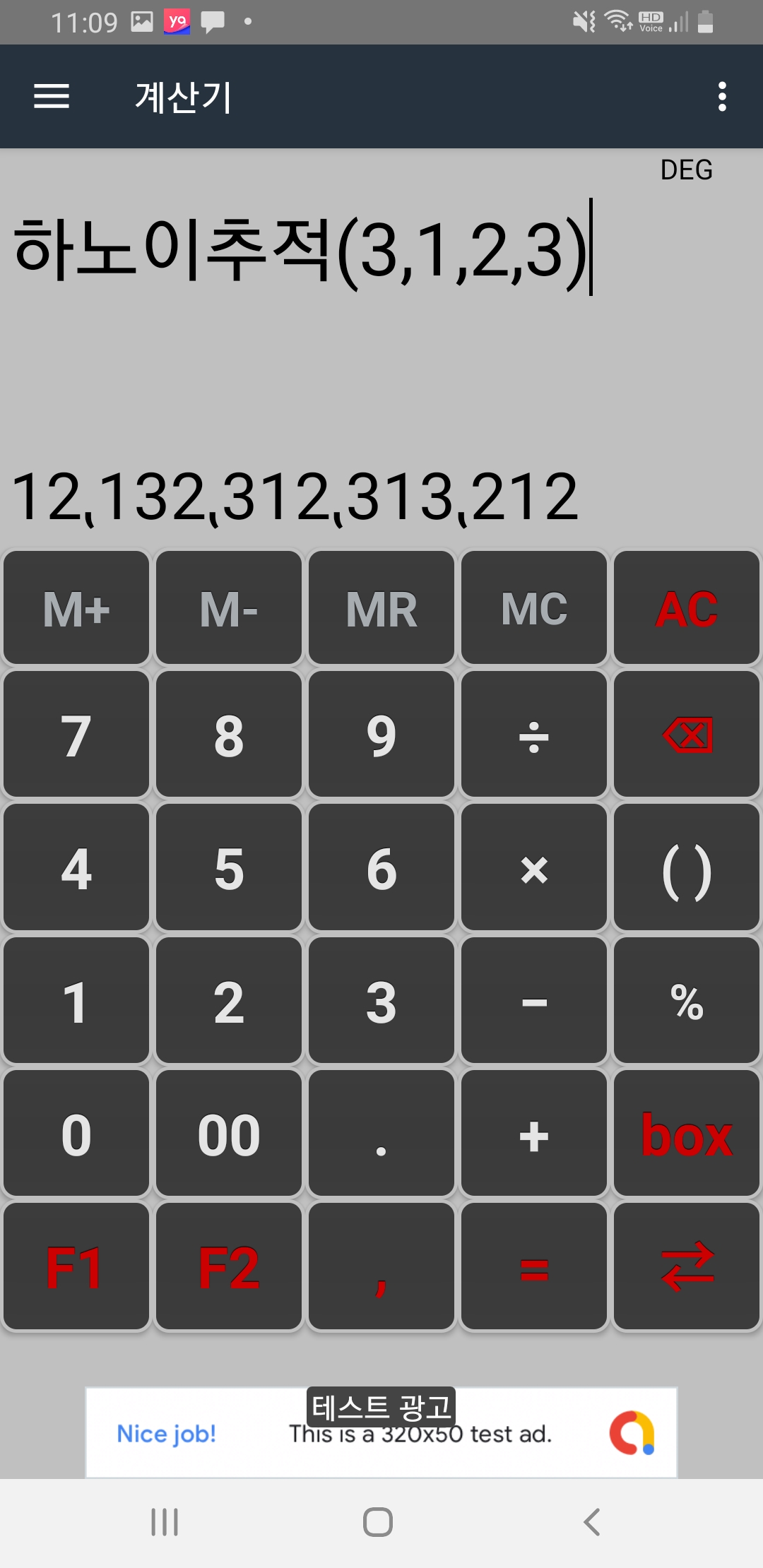
만약 하노이탑 퍼즐 장난감이 있으면 위 계산결과처럼 직접 옮겨보시기 바랍니다.
만약 원반 갯수가 5이면 아래 그림처럼 꽤 복잡한 이동이 필요할 것입니다.
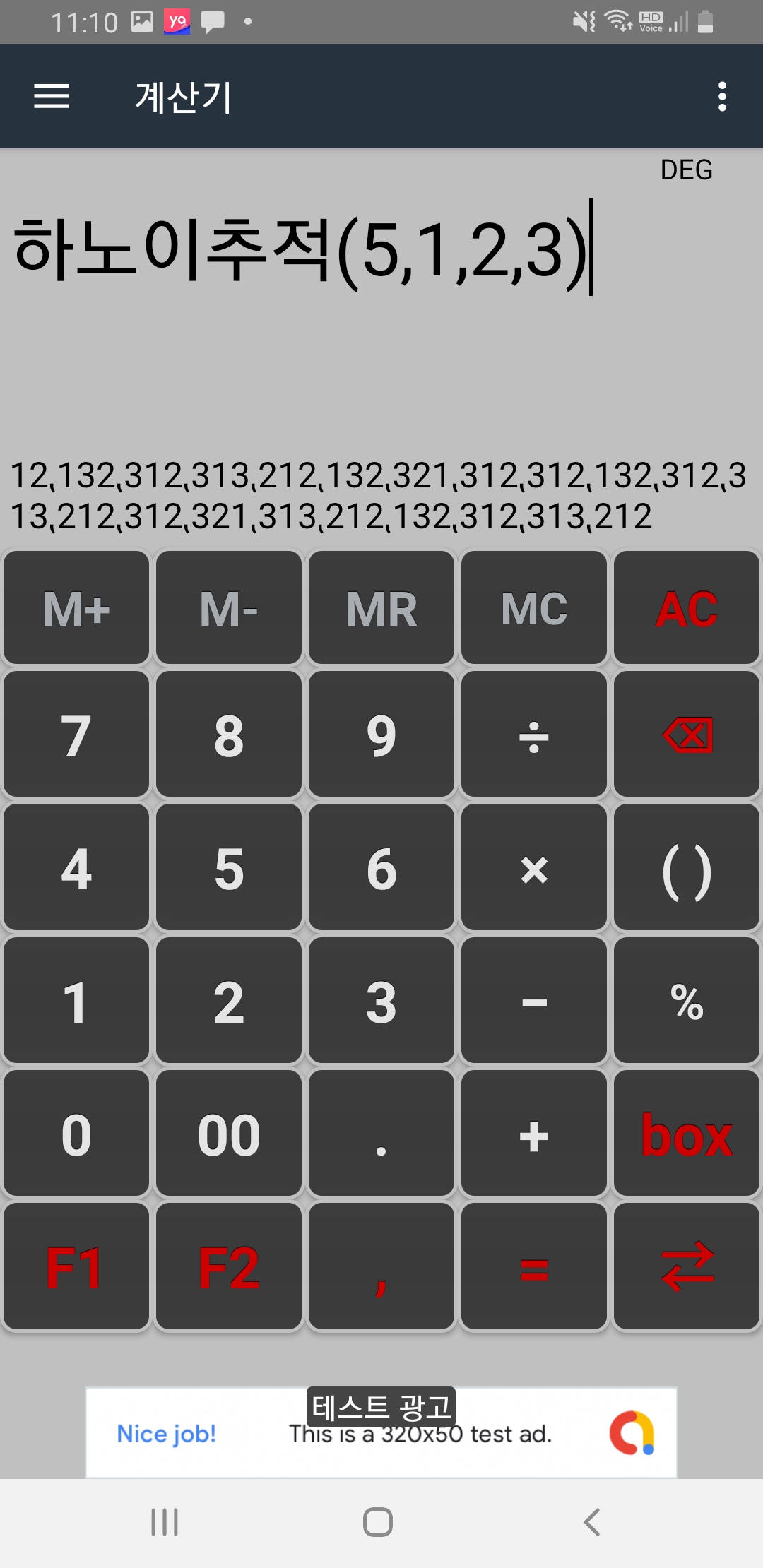
원반이 7개인 경우까지만 추적이 가능하고 그 이상은 너무 큰 숫자에다 너무 깊은 재귀로 인해 시스템 제약상 실행이 안되니 주의 하세요.
원반 7개인 경우는 아래 그림처럼 이동이 진행됩니다.
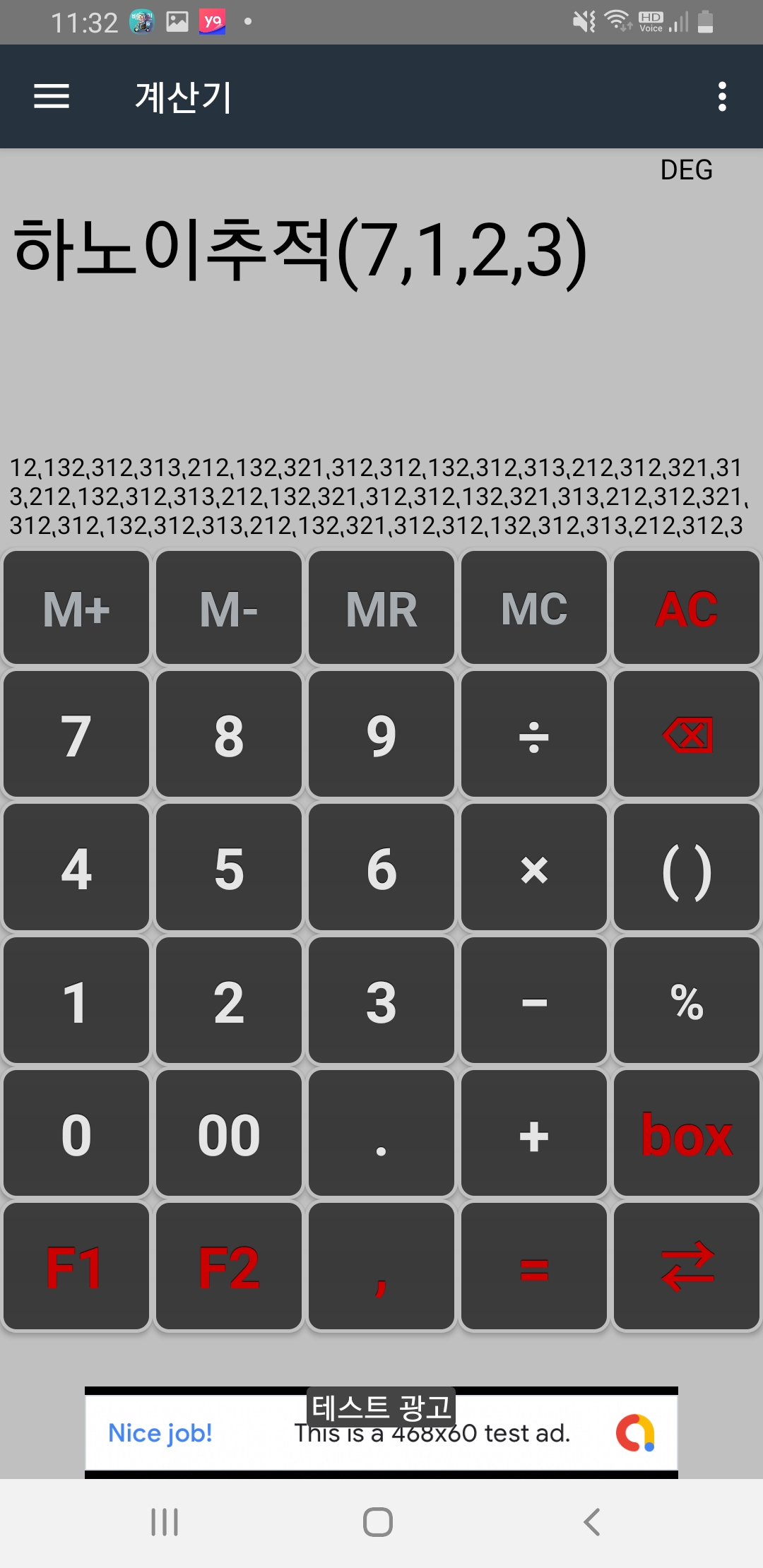
계산기록에 있는것을 표기해보면 아래와 같습니다.
하노이추적(7,1,2,3)=12⹁132⹁312⹁313⹁212⹁132⹁321⹁312⹁312⹁132⹁312⹁313⹁212⹁312⹁321⹁313⹁212⹁132⹁312⹁313⹁212⹁132⹁321⹁312⹁312⹁132⹁321⹁313⹁212⹁312⹁321⹁312⹁312⹁132⹁312⹁313⹁212⹁132⹁321⹁312⹁312⹁132⹁312⹁313⹁212⹁312⹁321⹁313⹁212⹁132⹁312⹁313⹁212⹁312⹁321⹁312⹁312⹁132⹁321⹁313⹁212⹁312⹁321⹁313⹁212⹁132⹁312⹁313⹁212⹁132⹁321⹁312⹁312⹁132⹁312⹁313⹁212⹁312⹁321⹁313⹁212⹁132⹁312⹁313⹁212
위 숫자를 둘씩 둘씩 끊어서 원반을 그 숫자 짝대로 옮기면 정확히 모든 원반을 옮길 수 있습니다.
12 13 23 12 31 32 12 13 23 21 31 23
12 13 23 12 31 32 12 31 23 21 31 32
12 13 23 12 31 32 12 13 23 21 31 23
12 13 23 21 31 32 12 31 23 21 31 23
12 13 23 12 31 32 12 13 23 21 31 23
12 13 23 12 31 32 12 31 23 21 31 32
12 13 23 12 31 32 12 31 23 21 31 23
12 13 23 21 31 32 12 31 23 21 31 32
12 13 23 12 31 32 12 13 23 21 31 23
12 13 23 12 31 32 12 31 23 21 31 32
12 13 23 12 31 32 12
현재 개발 중인 기능을 적용하면 위 숫자를 아래 그림과 같이 단어들로 치환할 수도 있습니다.
반복문으로 하노이 탑 추적하기
재귀 로직은 재귀를 이해하면 로직이 단순하고 강력하지만 컴퓨터의 입장에서는 로직을 계속 쌓아두고 계산을 수행하기때문에 로직이 너무 많이 쌓이면 컴퓨터가 스택오버플로우 라는 오류를 일으킵니다.
반면에 반복문을 사용하여 로직을 구현하면 로직을 쌓아두는 대신 자꾸 동일한 부분을 자꾸 자꾸 반복하기때문에 컴퓨터 입장에서는 반복 실행이 부담이 훨씬 덜한 계산방법입니다.
단점은 그 대신 로직이 복잡해져서 사람이 코드를 읽고 이해하기가 어렵다는 점입니다.
아래는 claude AI 에게 반복문으로 하노이 탑의 원반의 막대간 이동을 추적할 함수를 만들어 달라고 요청을 했고 아래와 같이 만들어 줬습니다.
여기서는 claude AI 가 다른 AI보다 일을 잘 처리하네요. 물론 버젼이 달라서 그럴 수도 있지만...
def hanoiMovesIterative(n,s,d,a){
var result=0;
var maxStackSize=100;
var stack=0;
var sp=0;
var diskArr=0;
var sourceArr=0;
var destArr=0;
var auxArr=0;
var stageArr=0;
var i=0;
while(i<maxStackSize){
diskArr=diskArr*10+0;
sourceArr=sourceArr*10+0;
destArr=destArr*10+0;
auxArr=auxArr*10+0;
stageArr=stageArr*10+0;
i=i+1;
}
var tempDisk=diskArr;
diskArr=diskArr*10+n;
var tempSrc=sourceArr;
sourceArr=sourceArr*10+s;
var tempDst=destArr;
destArr=destArr*10+d;
var tempAux=auxArr;
auxArr=auxArr*10+a;
var tempStg=stageArr;
stageArr=stageArr*10+0;
sp=sp+1;
while(sp>0){
var currDisk=diskArr%10;
diskArr=floor(diskArr/10);
var currSrc=sourceArr%10;
sourceArr=floor(sourceArr/10);
var currDst=destArr%10;
destArr=floor(destArr/10);
var currAux=auxArr%10;
auxArr=floor(auxArr/10);
var currStg=stageArr%10;
stageArr=floor(stageArr/10);
sp=sp−1;
if(currDisk==1){
result=result*100+currSrc*10+currDst;
}
elseif(currStg==0){
diskArr=diskArr*10+currDisk;
sourceArr=sourceArr*10+currSrc;
destArr=destArr*10+currDst;
auxArr=auxArr*10+currAux;
stageArr=stageArr*10+1;
sp=sp+1;
diskArr=diskArr*10+(currDisk−1);
sourceArr=sourceArr*10+currSrc;
destArr=destArr*10+currAux;
auxArr=auxArr*10+currDst;
stageArr=stageArr*10+0;
sp=sp+1;
}
elseif(currStg==1){
result=result*100+currSrc*10+currDst;
diskArr=diskArr*10+currDisk;
sourceArr=sourceArr*10+currSrc;
destArr=destArr*10+currDst;
auxArr=auxArr*10+currAux;
stageArr=stageArr*10+2;
sp=sp+1;
diskArr=diskArr*10+(currDisk−1);
sourceArr=sourceArr*10+currAux;
destArr=destArr*10+currDst;
auxArr=auxArr*10+currSrc;
stageArr=stageArr*10+0;
sp=sp+1;
}
}
return result;
}
일단 복잡해서 읽는건 생략하고 기존에 만들어진 재귀함수와 같은 결과를 내는지 체크해 보니 같은 결과를 내네요.
그래서 합격.
이 코드도 공장 페이지에 복사해서 붙여놓고 실행한 후 계산기에서 아래와 같이 계산하였습니다.
재귀함수로는 하지 못했던 원반이 9개인 경우 하노이 탑 원반의 막대간 이동 순서는 아래 그림과 같습니다.

계산기에 답이 다 안 나올 경우는 =을 누르면 계산기록 페이지에 결과가 제대로 저장됩니다.
계산기록 페이지의 결과는 아래와 같습니다.
도전해 보실 분들은 원반 9개짜리 하노이 탑 퍼즐로 아래 숫자를 둘씩 둘씩 묶어서 순서쌍대로 실험해 보셔도 재미있을 것입니다.
hanoiMovesIterative(9,1,2,3)=12⹁132⹁312⹁313⹁212⹁132⹁321⹁312⹁312⹁132⹁312⹁313⹁212⹁312⹁321⹁313⹁212⹁132⹁312⹁313⹁212⹁132⹁321⹁312⹁312⹁132⹁321⹁313⹁212⹁312⹁321⹁312⹁312⹁132⹁312⹁313⹁212⹁132⹁321⹁312⹁312⹁132⹁312⹁313⹁212⹁312⹁321⹁313⹁212⹁132⹁312⹁313⹁212⹁312⹁321⹁312⹁312⹁132⹁321⹁313⹁212⹁312⹁321⹁313⹁212⹁132⹁312⹁313⹁212⹁132⹁321⹁312⹁312⹁132⹁312⹁313⹁212⹁312⹁321⹁313⹁212⹁132⹁312⹁313⹁212⹁132⹁321⹁312⹁312⹁132⹁321⹁313⹁212⹁312⹁321⹁312⹁312⹁132⹁312⹁313⹁212⹁132⹁321⹁312⹁312⹁132⹁321⹁313⹁212⹁312⹁321⹁313⹁212⹁132⹁312⹁313⹁212⹁312⹁321⹁312⹁312⹁132⹁321⹁313⹁212⹁312⹁321⹁312⹁312⹁132⹁312⹁313⹁212⹁132⹁321⹁312⹁312⹁132⹁312⹁313⹁212⹁312⹁321⹁313⹁212⹁132⹁312⹁313⹁212⹁132⹁321⹁312⹁312⹁132⹁321⹁313⹁212⹁312⹁321⹁312⹁312⹁132⹁312⹁313⹁212⹁132⹁321⹁312⹁312⹁132⹁312⹁313⹁212⹁312⹁321⹁313⹁212⹁132⹁312⹁313⹁212⹁312⹁321⹁312⹁312⹁132⹁321⹁313⹁212⹁312⹁321⹁313⹁212⹁132⹁312⹁313⹁212⹁132⹁321⹁312⹁312⹁132⹁312⹁313⹁212⹁312⹁321⹁313⹁212⹁132⹁312⹁313⹁212⹁312⹁321⹁312⹁312⹁132⹁321⹁313⹁212⹁312⹁321⹁312⹁312⹁132⹁312⹁313⹁212⹁132⹁321⹁312⹁312⹁132⹁321⹁313⹁212⹁312⹁321⹁313⹁212⹁132⹁312⹁313⹁212⹁312⹁321⹁312⹁312⹁132⹁321⹁313⹁212⹁312⹁321⹁313⹁212⹁132⹁312⹁313⹁212⹁132⹁321⹁312⹁312⹁132⹁312⹁313⹁212⹁312⹁321⹁313⹁212⹁132⹁312⹁313⹁212⹁132⹁321⹁312⹁312⹁132⹁321⹁313⹁212⹁312⹁321⹁312⹁312⹁132⹁312⹁313⹁212⹁132⹁321⹁312⹁312⹁132⹁312⹁313⹁212⹁312⹁321⹁313⹁212⹁132⹁312⹁313⹁212⹁312⹁321⹁312⹁312⹁132⹁321⹁313⹁212⹁312⹁321⹁313⹁212⹁132⹁312⹁313⹁212⹁132⹁321⹁312⹁312⹁132⹁312⹁313⹁212⹁312⹁321⹁313⹁212⹁132⹁312⹁313⹁212
위 긴 숫자를 막대간에 옮기는 순서쌍대로 두 개 두 개씩 숫자들을 띄어 보면 아래와 같습니다.
12 13 23 12 31 32 12 13 23 21 31 23
12 13 23 12 31 32 12 31 23 21 31 32
12 13 23 12 31 32 12 13 23 21 31 23
12 13 23 21 31 32 12 31 23 21 31 23
12 13 23 12 31 32 12 13 23 21 31 23
12 13 23 12 31 32 12 31 23 21 31 32
12 13 23 12 31 32 12 31 23 21 31 23
12 13 23 21 31 32 12 31 23 21 31 32
12 13 23 12 31 32 12 13 23 21 31 23
12 13 23 12 31 32 12 31 23 21 31 32
12 13 23 12 31 32 12 13 23 21 31 23
12 13 23 21 31 32 12 31 23 21 31 23
12 13 23 12 31 32 12 13 23 21 31 23
12 13 23 21 31 32 12 31 23 21 31 32
12 13 23 12 31 32 12 31 23 21 31 23
12 13 23 21 31 32 12 31 23 21 31 23
12 13 23 12 31 32 12 13 23 21 31 23
12 13 23 12 31 32 12 31 23 21 31 32
12 13 23 12 31 32 12 13 23 21 31 23
12 13 23 21 31 32 12 31 23 21 31 23
12 13 23 12 31 32 12 13 23 21 31 23
12 13 23 12 31 32 12 31 23 21 31 32
12 13 23 12 31 32 12 31 23 21 31 23
12 13 23 21 31 32 12 31 23 21 31 32
12 13 23 12 31 32 12 13 23 21 31 23
12 13 23 12 31 32 12 31 23 21 31 32
12 13 23 12 31 32 12 31 23 21 31 23
12 13 23 21 31 32 12 31 23 21 31 23
12 13 23 12 31 32 12 13 23 21 31 23
12 13 23 21 31 32 12 31 23 21 31 32
12 13 23 12 31 32 12 31 23 21 31 23
12 13 23 21 31 32 12 31 23 21 31 32
12 13 23 12 31 32 12 13 23 21 31 23
12 13 23 12 31 32 12 31 23 21 31 32
12 13 23 12 31 32 12 13 23 21 31 23
12 13 23 21 31 32 12 31 23 21 31 23
12 13 23 12 31 32 12 13 23 21 31 23
12 13 23 12 31 32 12 31 23 21 31 32
12 13 23 12 31 32 12 31 23 21 31 23
12 13 23 21 31 32 12 31 23 21 31 32
12 13 23 12 31 32 12 13 23 21 31 23
12 13 23 12 31 32 12 31 23 21 31 32
12 13 23 12 31 32 12
함수계산기의 코딩 기능을 활용해 다른 많은 흥미로운 문제들을 풀어보세요.
'함수계산기' 카테고리의 다른 글
| D 데이 계산함수 만들기 (2) | 2025.04.01 |
|---|---|
| 날짜와 요일 계산하는 함수 만들기 (0) | 2025.03.31 |
| 할부금 계산하는 함수 만들어 보기 (0) | 2025.03.28 |
| 생활 속의 연립방정식 (0) | 2025.03.28 |
| 정적분 근사값 구하는 함수 만들기 (0) | 2025.03.27 |